Specify a Distribution • distionary

library(distionary)

This vignette covers the first goal of distionary: to provide a framework for creating a distribution, either one of the built-in distributions, or your own.

Built-In Distribution Families

All distribution families found in the stats package are made available with distionary, along with a few others. All families are shown in the following table.

Distribution	`distionary` Function	Has counterpart in `stats`
Bernoulli	`dst_bern()`	Yes
Beta	`dst_beta()`	Yes
Binomial	`dst_binom()`	Yes
Cauchy	`dst_cauchy()`	Yes
Chi Squared	`dst_chisq()`	Yes
Degenerate	`dst_degenerate()`	No
Exponential	`dst_exp()`	Yes
F	`dst_f()`	Yes
Gamma	`dst_gamma()`	Yes
Geometric	`dst_geom()`	Yes
Generalised Extreme Value (GEV)	`dst_gev()`	No
Generalised Pareto (GPD)	`dst_gpd()`	No
Hypergeometric	`dst_hyper()`	Yes
Log Normal	`dst_lnorm()`	Yes
Log Pearson Type III	`dst_lp3()`	No
Negative Binomial	`dst_nbinom()`	Yes
Normal	`dst_norm()`	Yes
Pearson Type III	`dst_pearson3()`	No
Poisson	`dst_pois()`	Yes
Student t	`dst_t()`	Yes
Uniform	`dst_unif()`	Yes
Weibull	`dst_weibull()`	Yes

In addition, there is a special “Null” distribution object akin to a missing or unknown distribution. This is useful, for example, if an algorithm fails to return a distribution: instead of throwing an error, a Null distribution can be returned.

# Make a Null distribution.
null <- dst_null()
# Inspect
null
#> Null distribution (NA)

A Null distribution always evaluates to NA:

mean(null)
#> [1] NA
eval_pmf(null, at = 1:4)
#> [1] NA NA NA NA

Distributions with a counterpart in the stats package use the same functions from the package and the same parameter names. For instance, take a look at the source code defining the Normal distribution to see that the representations wrap the stats::*norm() family of functions.

dst_norm
#> function (mean, sd) 
#> {
#>     checkmate::assert_numeric(mean, len = 1)
#>     checkmate::assert_numeric(sd, 0, len = 1)
#>     if (is.na(mean) || is.na(sd)) {
#>         return(dst_null())
#>     }
#>     distribution(.parameters = list(mean = mean, sd = sd), density = function(x) stats::dnorm(x, 
#>         mean = mean, sd = sd), cdf = function(x) stats::pnorm(x, 
#>         mean = mean, sd = sd), quantile = function(p) stats::qnorm(p, 
#>         mean = mean, sd = sd), realise = function(n) stats::rnorm(n, 
#>         mean = mean, sd = sd), survival = function(x) stats::pnorm(x, 
#>         mean = mean, sd = sd, lower.tail = FALSE), mean = mean, 
#>         median = mean, variance = sd^2, stdev = sd, skewness = 0, 
#>         kurtosis_exc = 0, range = c(-Inf, Inf), .name = "Normal", 
#>         .vtype = "continuous")
#> }
#> <bytecode: 0x56293eb8ee40>
#> <environment: namespace:distionary>

User-Defined Distributions

You can make your own distribution using the distribution() function. Provide it with name-value pairs that will be stored with the object in a list. Some names have a special interpretation in distionary in that they may be leveraged to compute other properties that aren’t specified in distribution(). These special names are:

Any distributional representation * invoked by eval_*() (e.g., quantile for eval_quantile()).
Any property (e.g., mean for mean())

See the Evaluate a Distribution vignette for more details on these evaluation functions.

For this version of distionary, it is mandatory to specify at least cdf in order for non-specified properties to be evaluated. For continuous or discrete distributions, density or pmf may also be needed.

Optionally, you can also specify an entry for .parameters, which should be a named list of parameters that define the distribution. These parameters are never used for distribution calculations, but are sometimes useful to keep track of for analysis. It is intended that a future version of distionary will refer to these parameters for its calculations, but will not break existing code.

Here is an example distribution.

# Make a continuous distribution
linear <- distribution(
  density = function(x) {
    d <- 2 * (1 - x)
    d[x < 0 | x > 1] <- 0
    d
  },
  cdf = function(x) {
    p <- 2 * x * (1 - x / 2)
    p[x < 0] <- 0
    p[x > 1] <- 1
    p
  },
  g = 9.81,
  another_representation = function(x) x^2,
  .vtype = "continuous",
  .name = "My Linear",
  .parameters = list(a = 1)
)
# Inspect
linear
#> My Linear distribution (continuous)
#> --Parameters--
#> a 
#> 1

The usual evaluation framework can now be accessed. For example, the CDF and mean can be evaluated, even though the mean has not been specified.

eval_cdf(linear, at = c(0.2, 0.5, 0.7))
#> [1] 0.36 0.75 0.91
mean(linear)
#> [1] 0.3333333

These quantities can be invoked by the more general function eval_property().

eval_property(linear, "cdf", c(0.2, 0.5, 0.7))
#> [1] 0.36 0.75 0.91
eval_property(linear, "mean")
#> [1] 0.3333333

eval_property() is a useful function for accessing quantities that are not built-in to distionary, like g and another_representation in this example.

eval_property(linear, "another_representation", 1:4)
#> [1]  1  4  9 16
eval_property(linear, "g")
#> [1] 9.81

Network of Properties

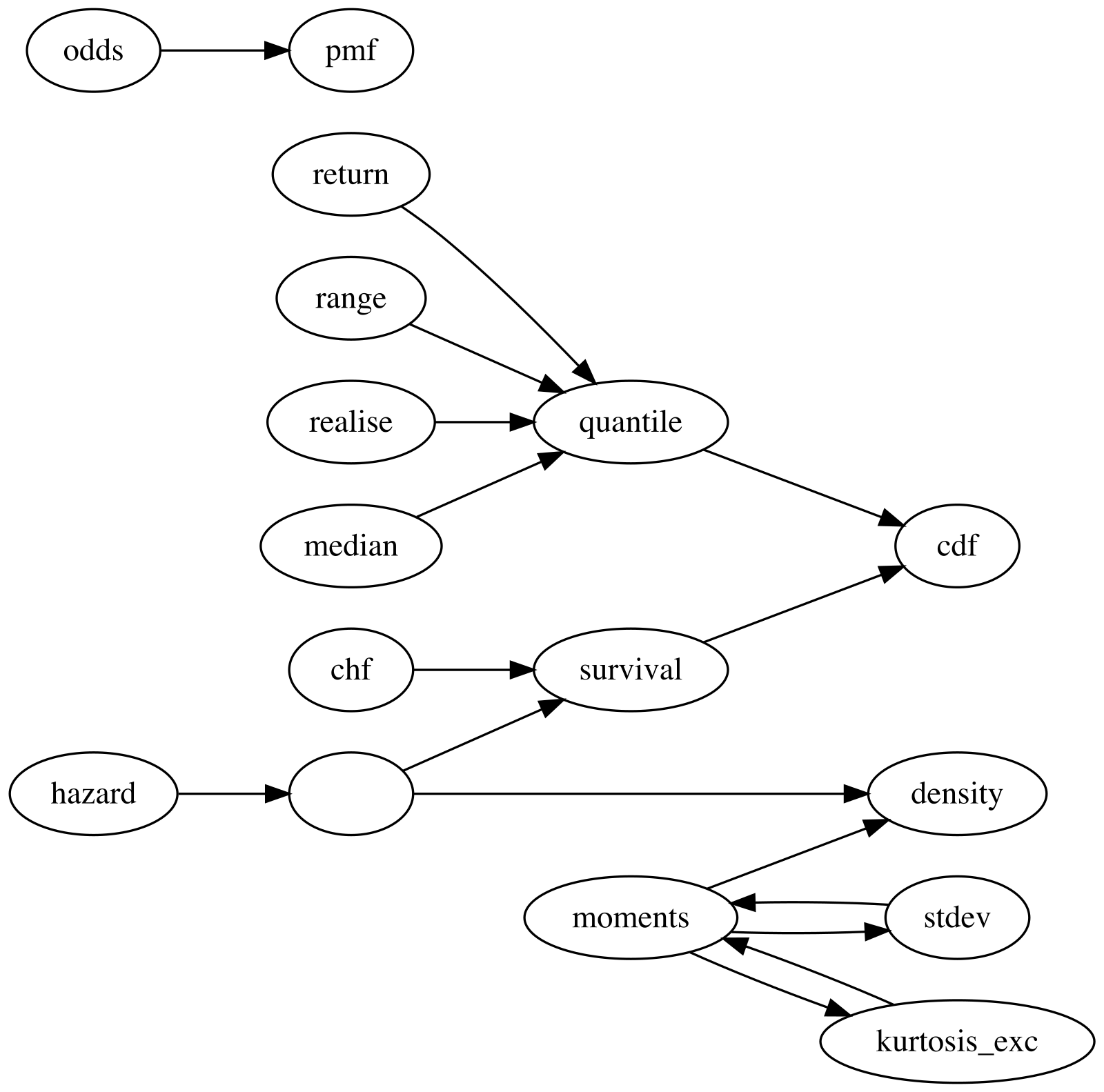
The current version of distionary derives distribution properties from other properties according to the following network. An arrow from one property to another indicates that the first property can be calculated from the second. For example, quantile can be calculated from cdf, and mean can be calculated from density.